Why UndersmoothedUnfolding?

Coverage as a function of regularization strength

UndersmoothedUnfolding an extension for the unfolding software TUnfoldV17.8 2 written by Stefan Schmitt. TUnfold implements Tikhonov regularization for unfolding smeared data from particle detectors. However, as demonstrated by Kuusela (2016) 1, the resulting confidence intervals may seriously underestimate the true uncertainty in the unfolded space, unless care is taken in the choice of the regularization strength \(\tau\).

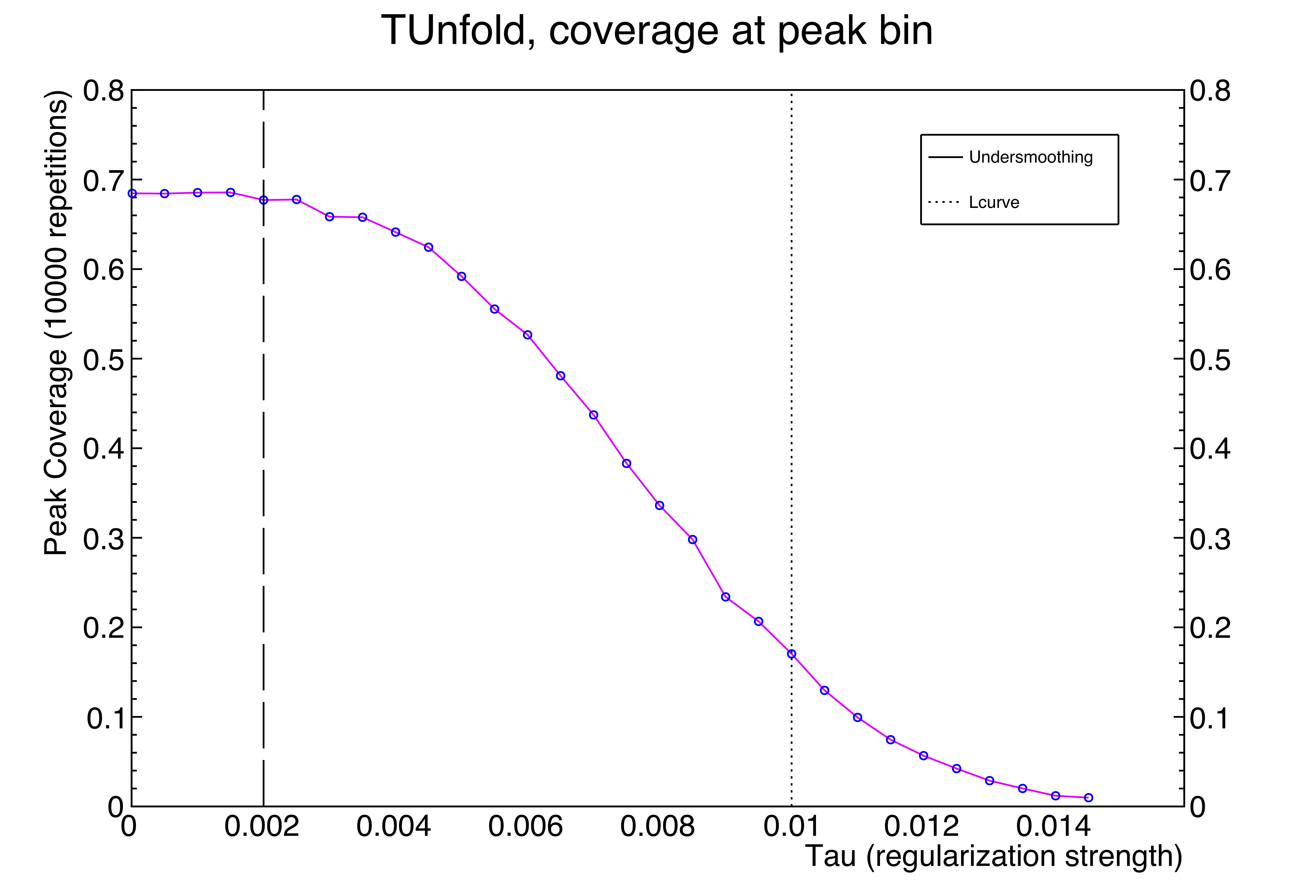
_images/coverage_peak_bin_curvature.png

Coverage is empirically obtained with 10,000 independent realizations of the data.

The plot above illustrates the empirical coverage at the peak bin (with highest \(y\)-value) for various values of the regularization strength in the two Gaussian peaks example described below. Coverage starts at the nominal level (68 %) when there is no regularization. However, as the regularization strength increases, coverage gradually decreases to zero.

The first vertical line indicates the average regularization strength chosen by UndersmoothedUnfolding::UndersmoothTau, and the corresponding coverage is near the nominal level (68 %). On the other hand, the second vertical line, corresponding to the average regularization strength chosen by TUnfold::ScanLcurve, shows serious undercoverage at around 20%. This result shows that TUnfold::ScanLcurve regularizes too strongly from the perspective of uncertainty quantification, while UndersmoothedUnfolding::UndersmoothTau has chosen a regularization strength that results in better-calibrated uncertainties.

Coverage demonstration I: Two Gaussian peaks

The first test case we consider has two Gaussian peaks on top of a uniform background, resembling situations where invariant mass peaks are observed on top of some background events. The observations are smeared with Gaussian noise, resulting in a Gaussian deconvolution problem.

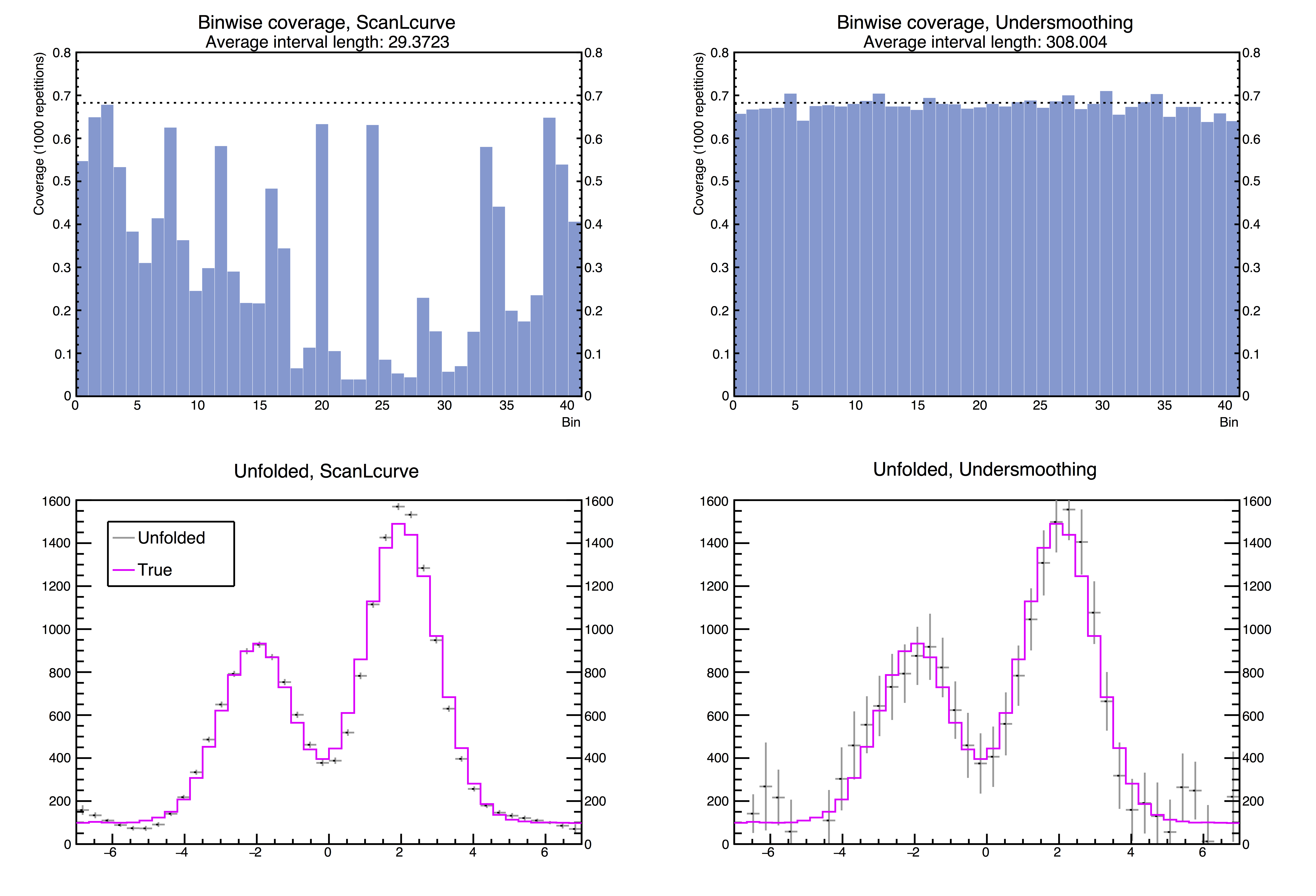
_images/undersmooth_demo_twopeaks.png

The coverage is estimated by repeating the unfolding 1,000 times with independent realizations of the data. The average confidence interval length for each method is indicated above the top plots.

The top two plots compare the performance of the unfolded confidence intervals when \(\tau\) is chosen using TUnfold::ScanLcurve and the algorithm UndersmoothedUnfolding::UndersmoothTau provided by this software. The tolerance \(\epsilon\) is set to 0.01, so the intervals from UndersmoothTau should have 67% coverage. The bottom plots show one realization of the unfolded confidence intervals for each method. The confidence intervals provided by TUnfold::ScanLcurve are too short and suffer from drastic undercoverage, while the intervals provided by UndersmoothedUnfolding::UndersmoothTau have nearly nominal coverage without being excessively long.

Coverage demonstration II: Steeply falling spectrum

The second test case we consider has a steeply falling particle spectrum, and we use the inclusive jet transverse momentum spectrum 3 as an example. Observing a jet, a collimated stream of energetic particles, in an LHC particle detector implies the creation of a quark or a gluon, and analyzing the properties of these jets is an important test of the Standard Model of particle physics. In this example, the smearing kernel is Gaussian with a variance that changes along the \(x\)-axis. See Kuusela (2016) 1 for a more detailed description of the experiment setup.

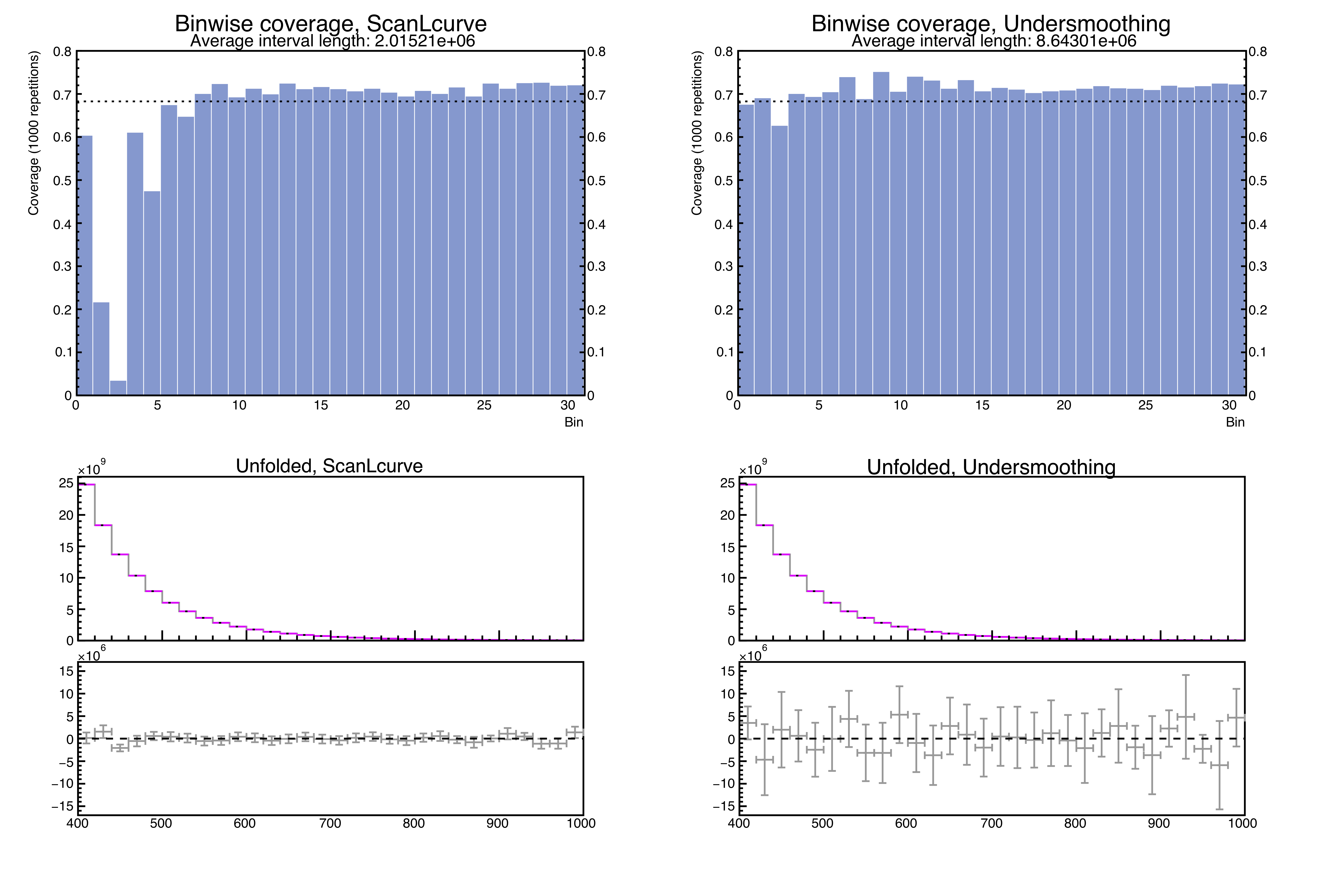
_images/undersmooth_demo_incjets.png

The coverage is estimated by repeating the unfolding 1,000 times with independent realizations of the data. The average confidence interval length for each method is indicated above the top plots.

Again, we see that the confidence intervals provided by TUnfold::ScanLcurve suffer from drastic undercoverage especially on the left side of the spectrum, while the intervals provided by UndersmoothedUnfolding::UndersmoothTau have nearly nominal coverage.

1(1,2)

  1. Kuusela, “Uncertainty quantification in unfolding elementary particle spectra at the Large Hadron Collider”, PhD thesis, EPFL (2016)

2

  1. Schmitt, “TUnfold, an algorithm for correcting migration effects in high energy physics”, Journal of Instrumentation 7 (2012)

3

CMS Collaboration, “Measurement of the Inclusive Jet Cross Section in \(pp\) Collisions at \(\sqrt{s} = 7\) TeV”, Physical Review D 107 (2011)