A Catalyst Framework for the Quantum Linear System Problem via the Proximal Point Algorithm

This blog post is about my recent work on solving quantum linear system problem with (classical) proximal point method. This post is written with my advisor Prof. Tasos Kyrillidis, and can also be found here. This is a joint work with Prof. Tasos Kyrillidis and Prof. Nai-Hui Chia.

Introduction

Solving systems of linear equations is essential in numerous applications, from scientific computing to machine learning. Classical algorithms like Gaussian elimination and iterative methods scale poorly with the problem size, often rendering large-scale problems intractable. Quantum algorithms offer a potential breakthrough by reducing the dependence on the problem dimensions from polynomial to logarithmic, as demonstrated by the Harrow-Hassidim-Lloyd (HHL) algorithm. Nevertheless, the performance of quantum algorithms is severely impacted by the condition number $\kappa$ of the input matrix, which measures the sensitivity of the system to numerical errors. High-condition numbers can significantly degrade the efficiency of quantum solutions, a challenge we address in this study.

Our approach leverages the classical proximal point algorithm (PPA), a method known for improving the conditioning of the problem in optimization tasks. By adapting the PPA to the quantum linear system problem (QLSP), we introduce a framework that enhances the performance of existing quantum linear system solvers. The key innovation lies in modifying the matrix to be inverted, thus reducing the effective condition number and improving convergence rates. This method can be seamlessly integrated with existing quantum solvers, providing a versatile tool for tackling a broader class of linear system problems.

The Quantum Linear System Problem (QLSP)

The Quantum Linear System Problem (QLSP) aims to prepare a quantum state proportional to the solution vector $x^\star$ of a linear system $Ax=b$. This task is central to many quantum algorithms, including those for solving differential equations, machine learning, and optimization problems. Existing quantum algorithms, such as the HHL algorithm, achieve significant speedups over classical methods by reducing the complexity from polynomial to logarithmic in the problem dimension $N$. However, their performance is often limited by the condition number $\kappa$ of the matrix $A$.

The condition number $\kappa$ is defined as the ratio of the largest to the smallest singular value of $A$. High-condition numbers indicate ill-conditioned systems that are susceptible to numerical errors, which can significantly slow down convergence and affect the final accuracy. Addressing this limitation is crucial for extending the applicability of quantum algorithms to real-world problems, which often involve ill-conditioned matrices.

A proper definition of the QLSP problem is as follows:

Our proposed framework leverages the proximal point algorithm (PPA) to address this challenge. By iteratively refining the solution through a modified matrix inversion process, our approach effectively preconditions the system, reducing the impact of high-condition numbers. This approach not only improves convergence rates but also broadens the range of problems that quantum algorithms can efficiently solve.

Our Contributions

We present a novel meta-algorithmic framework that enhances the performance of existing quantum linear system solvers. Our contributions are as follows:

• Improved Condition Number: Our method reduces the effective condition number from $\kappa$ to $\frac{\kappa(1+\eta)}{\kappa + \eta}$, where $\eta$ is a tunable parameter. This reduction alleviates the dependence of the algorithm on the condition number, leading to faster convergence.
• Flexibility: The proposed framework is versatile, allowing different QLSP solvers to be used as subroutines. This flexibility enables users to choose the most appropriate solver for their specific problem.
• Tunable Parameter $\eta$: By carefully selecting the parameter $\eta$, users can balance the trade-off between runtime and approximation error, optimizing overall algorithmic complexity.

Our approach stands out by directly approximating the solution vector $x^\star = A^{-1} b$ through iterative refinement. This is in contrast to existing methods that focus on approximating the inverse of the coefficient matrix $A$. By inverting a (normalized) modified matrix $I + \eta A$, our algorithm effectively preconditions the system, resulting in a better-conditioned problem that converges more rapidly.

Algorithmic and Theoretical Intuition

Our proposed algorithm employs the proximal point algorithm (PPA) to solve the QLSP. The core idea is to invert the (normalized) modified matrix $I + \eta A$ instead of the original matrix $A$, thus improving the system’s conditioning. The algorithm proceeds as follows:

• Initialization: Start with an initial guess $x_0 + \eta b$ for the solution vector.
• Matrix Modification: Modify the matrix $A$ to $\frac{I + \eta A}{|| I + \eta A ||}$.
• Refinement: Apply any existing QLSP solver to invert the modified matrix and apply to the initial guess.

The convergence rate and error bounds of our algorithm are rigorously analyzed. By carefully choosing the parameter $\eta$, the algorithm balances the trade-off between runtime and approximation error. Our theoretical analysis demonstrates that the proposed method achieves faster convergence and greater accuracy than existing quantum solvers, especially for ill-conditioned problems.

We also provide a detailed complexity analysis, showing that our method significantly reduces the dependence on the condition number $\kappa$. Please check our paper for the complete and detailed theoretical analysis.

Empirical observations over theory

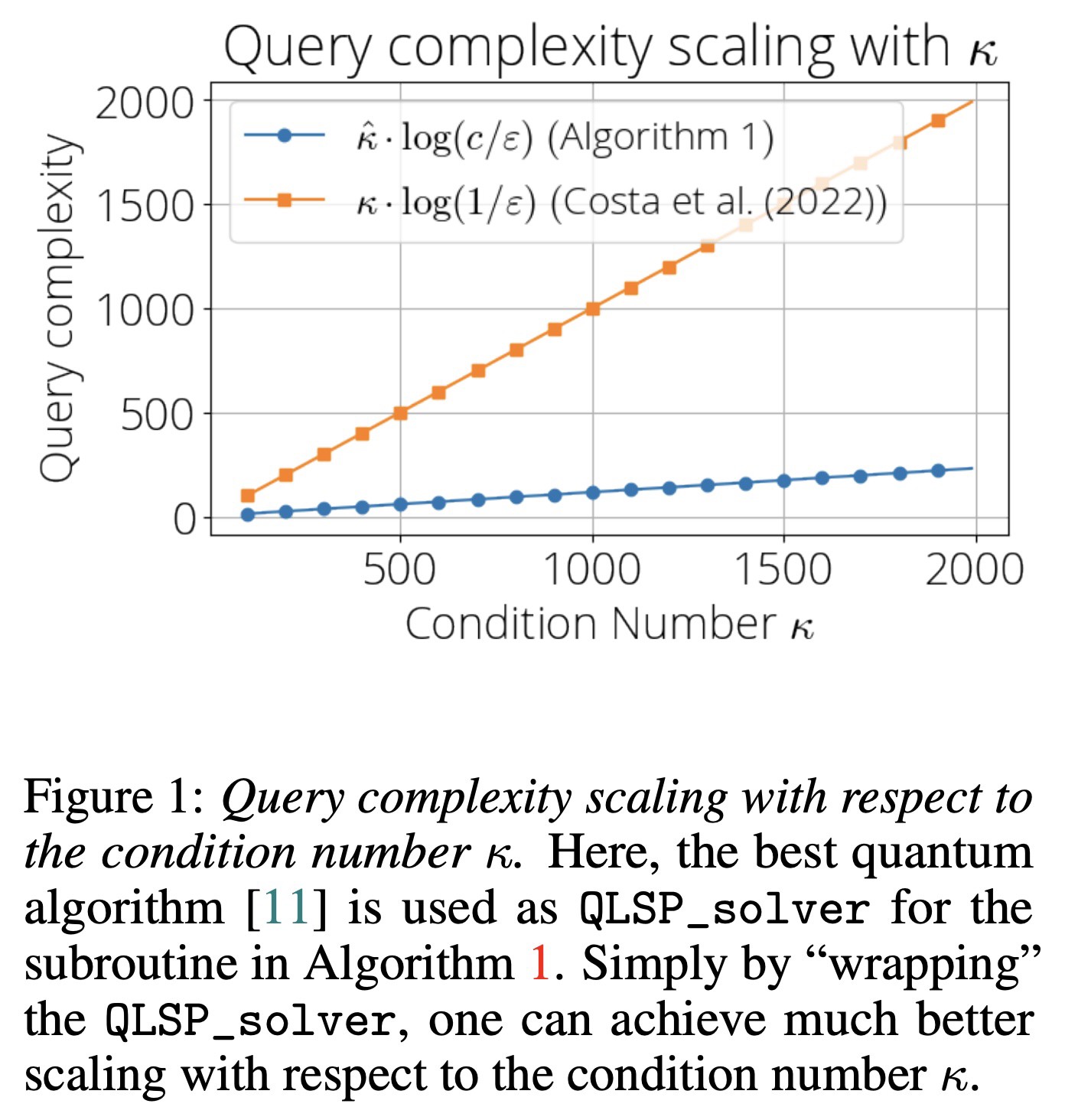
In Figure 1, we show how the query complexity scales as a function of the condition number $\kappa$. The orangle line is the state-of-the-art QLSP solver based on the discrete adiabatic theorem. Simply by “wrapping” the original QLSP solver with our proposed method, the query complexity to achieve a fixed accuracy improves as $\kappa$ increases.

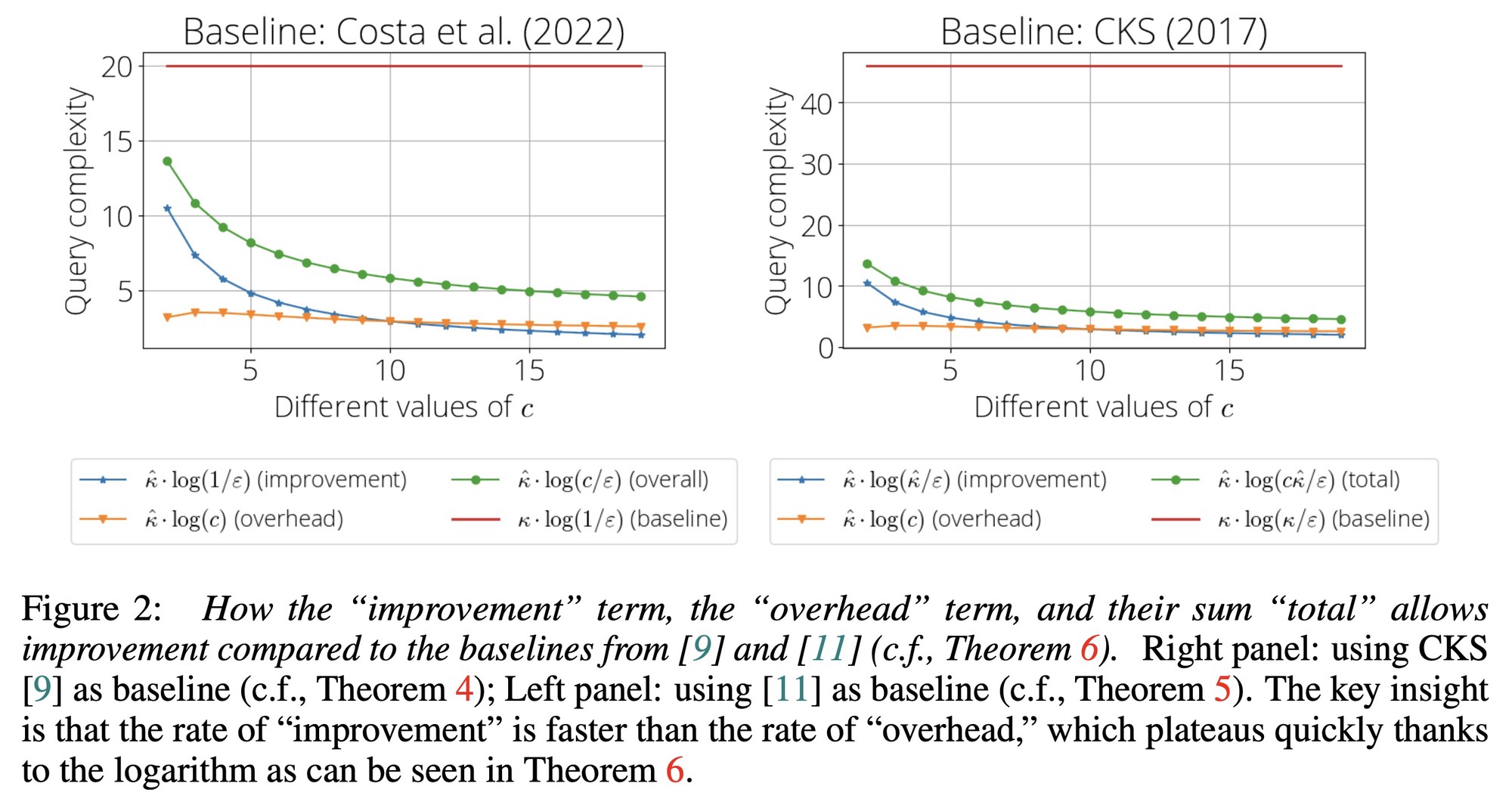
In Figure 2, we show, based on our theoretical analysis, the breakdown of the “improvement” and the “overhead” for two different QLSP solvers as subroutines.

Conclusions and Future Work

Our proposed framework significantly alleviates the dependence on the condition number in solving the Quantum Linear System Problem (QLSP). By leveraging the proximal point algorithm (PPA), we introduce a meta-algorithm that enhances the performance of existing quantum solvers, broadening their applicability to more challenging, ill-conditioned problems.

Future work will explore several promising directions:

• Multi-step PPA Implementation: Extending the algorithm to multi-step PPA implementations could further improve convergence rates and reduce runtime. This involves developing efficient methods for handling multiple iterations of the modified matrix inversion.
• Warm Starting: Investigating strategies for better initialization (warm starting) can lead to improved convergence. This may involve using prior knowledge about the solution or leveraging other quantum or classical solvers to provide a good starting point.
• Hybrid Approaches: Combining our framework with other optimization techniques, such as quantum-inspired algorithms, could yield even more efficient solvers.

Our work opens new avenues for research in quantum computing and optimization, providing a robust foundation for developing more advanced algorithms that can tackle a wider range of problems.